УЗО против дифавтомата – что лучше?
← Дешевле, но лучше? Да, это реально! || Распределительные щиты Univers с силовыми и слаботочными модулями →
УЗО против дифавтомата – что лучше?
Оговоримся сразу, что название было задумано другое — «Решение электрической схемы на УЗО или дифавтоматах – что лучше?», и оно звучит правильнее. Но поскольку запросы в поисковиках задаются именно такие, как в названии во главе, решили его не менять.
Итак, УЗО защищает жизнь человека при его прикосновении к токоведущим частям на которых имеется фазное напряжение. УЗО в момент прикосновения должно отключиться, сохранив человеку жизнь. Кроме того, протекание тока через не предназначенные для этого материалы может привести к возгоранию. В зданиях с ветхой электропроводкой пожары от повреждения изоляции случаются довольно часто. Тогда УЗО выполняет противопожарную функцию. Помним, что УЗО не защищает от перегрузки и короткого замыкания, для такой защиты УЗО устанавливают с одним автоматом или группой автоматических выключателей.
Однако когда мы сравниваем УЗО с группой автоматических выключателей и группу дифавтоматов для группы линий, сравнение уже не в пользу дифавтомата. Почему? Потому что становится актуальной стоимость решения. А оно лучше у УЗО с группой автоматов. Автоматический выключатель значительно дешевле дифавтомата, а УЗО можно поставить общее не на один автомат, а на группу. При том, что функционал решения будет таким же, как в случае с группой дифавтоматов.
Как работает УЗО
На схеме УЗО изображен человек, который прикосновением к токоведущему проводнику создал ток утечки. Сразу возникла разница между входящим и выходящим током, и когда эта разница достигает 30 мА, дифференциальный трансформатор формирует сигнал на расцепитель, который отключает линию, и сохраняет человеку жизнь.
Следующая схема отображает наглядную разницу в подключение УЗО и группы автоматических выключателей и подключения группы дифференциальных выключателей.
Итак, по стоимости первое решение (на УЗО) будет ниже, чем второе, т.к. дифавтомат – дорогое устройство.
- Кроме того есть другие различия:
 В решении с УЗО и группой автоматов необходимо еще коммутировать приборы между собой.
В решении с УЗО и группой автоматов необходимо еще коммутировать приборы между собой.Мы считаем, что решение на УЗО и группе автоматических выключателей рациональнее и правильнее применять при распределении тока по четырем и более линиям. Если линий меньше, несколько дифавтоматов станут простым и однозначным решением по защите цепи. Самое главное, правильно подключить все приборы и обеспечить надежную защиту от пожара или удара током.
Если линий меньше, несколько дифавтоматов станут простым и однозначным решением по защите цепи. Самое главное, правильно подключить все приборы и обеспечить надежную защиту от пожара или удара током.
Дифференциальный автомат. Назначение и принцип работы дифференциального автомата ~ Электрик в квартире и частном доме.
Дифференциальный автоматический выключатель представляет собой уникальное устройство, в котором одновременно сочетаются функции автоматического выключателя и защитные свойства УЗО.Также устройство осуществляет защиту электрической сети от коротких замыканий и перегрузок, выполняя функции автоматического выключателя.
Конструкция устройства
Конструктивно диф автоматы из состоят рабочей и защитной части.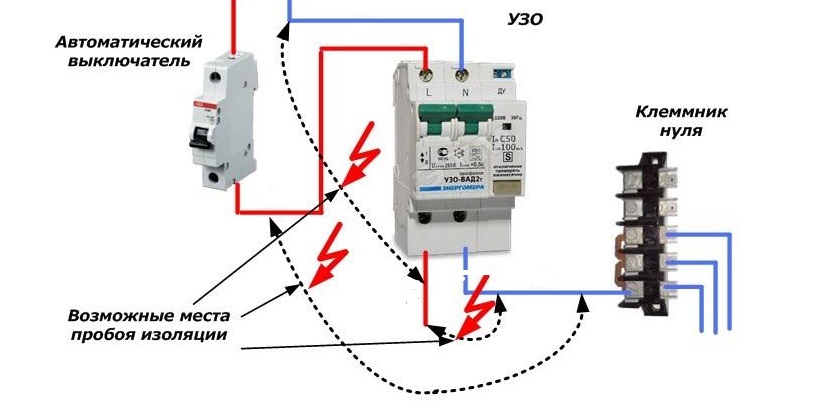
Рабочая часть представляет собой автоматический выключатель, в котором имеется специальный механизм независимого расцепления и рейка сброса с помощью внешнего механического воздействия. В различных типах диф автоматов устанавливаются четырехполюсные или двухполюсные автоматические выключатели.
Дифференциальный автомат, как и обычный автоматический выключатель, оборудован двумя расцепителями:
- — электромагнитный расцепитель отключает линию электропитания в случае короткого замыкания;
- — тепловой расцепитель срабатывает в случае возникновения перегрузки защищаемой группы.
Для обеспечения питания модуля защиты от электрического тока он включается последовательно с автоматическим выключателем.
В модуле защиты от электрического тока имеются некоторые дополнительные устройства, среди которых дифференциальный трансформатор, обнаруживающий остаточный электрический ток, а также электронный усилитель с катушкой электромагнитного сброса.
| Для проверки исправности модуля дифференциальной защиты на корпусе устройства расположена специальная кнопка «Тест». При нажатии на эту кнопку создается искусственный ток утечки и автомат (если он исправен) должен отключиться. |
Как работает диф автомат
В диф автомате, как и в устройстве защитного отключения, в качестве датчика утечки тока применяется специальный трансформатор. Работа этого трансформатора основана на изменении дифференциального тока в проводниках, подающих электрическую энергию на электроустановку, на которой обеспечивается защита.Ток утечки отсутствует, если нет повреждений изоляции электропроводки или к токоведущим частям установки никто не прикасается.
 В этом случае в нулевом и фазном проводе нагрузки будут протекать равные токи.
В этом случае в нулевом и фазном проводе нагрузки будут протекать равные токи.Этими токами в магнитном сердечнике трансформатора тока наводятся встречно направленные равные магнитные потоки. В результате этого ток вторичной обмотки равен нулю и чувствительный элемент – магнитоэлектрическая защелка не срабатывает.
В случае возникновения утечки, к примеру, если человек случайно прикоснется к фазному проводнику или при нарушении изоляционных свойств диэлектрика, происходит нарушение баланса тока и магнитных потоков.
Во вторичной обмотке возникает электрический ток, который приводит в действие магнитоэлектрическую защелку. Сработавшая защелка воздействует на механизм, расцепляющий автомат и контактную систему.
Где применяются диф автоматы
Дифференциальный автомат может с успехом применяться в однофазных и трехфазных сетях переменного тока. Эти устройства способствуют значительному повышению уровня безопасности в процессе постоянной эксплуатации различных электроприборов.
Кроме этого, дифференциальные автоматические выключатели способствуют предотвращению пожаров, вызванных возгоранием изоляции токоведущих частей некоторых электрических приборов.
Как работает УЗО – принцип работы и назначение
Главная » Все новости
30.06.2021
Сегодня практически в каждом доме и квартире можно встретить такой элемент как автомат. Автоматические выключатели помогают защитить наше жилье, офис либо производственное помещение от неприятных последствий короткого замыкания и перегрузок в электросети. Также подобные элементы защищают человека от поражения электрическим током, предотвращают возникновение возгорания и замыкания.
Какие функции выполняет устройство защитного отключения (УЗО)?
- В случае возникновения неисправности в электросети защищает человека от удара электрическим током.
- Отключает напряжение при нечаянном касании к токоведущим участкам электроустановки при возникновении утечки тока.
- Защищает электропроводку от возгорания.

Сегодня на рынке появилась современная альтернатива УЗО – дифференциальный автомат, которые совместили в себе особенности УЗО и автомата. Кроме того, подобные модели автоматов имеют небольшие габариты, за счет чего гораздо меньше занимают места в распределительных щитах.
Принцип работы УЗО
Принцип функционирования устройства защитного отключения основывается на реакции датчика тока на меняющуюся входящую величину дифференциального тока в проводниках. В качестве датчика тока используют трансформатор тока, выполненного в форме тороидального сердечника. Особо чувствительным элементом является уставка по току срабатывания. Контролирующее реле отвечает за размыкание электрической цепи. В современных моделях УЗО вместо контролирующего реле используют специальную электронную схему.
Теперь давайте разберемся из каких составляющих компонуется исполнительный механизм:
- контактная группа – подбирается модель, способная противостоять максимальному значению тока;
- пружины, которые размыкают электрическую цепь при возникновении аварийных ситуаций и сбоев в процессе работы.

Осуществить самостоятельную проверку исправной работы УЗО можно, нажав на клавишу «Тест». В данном случае производится контролируемая утечка тока, которая приводит к сработке УЗО. Провести проверку вполне реально самостоятельно, для этого вам не придется прибегать к помощи электриков. Настоятельно советуем проводить проверку исправности работы устройства защитного отключения один раз в месяц. Осуществить более тщательную проверку можно при помощи специального прибора, измеряющего ток и время срабатывания УЗО.
Если электропроводка находится в нормальном рабочем состоянии, тогда ток будет протекать навстречу параллельно, создавая во вторичной обмотке трансформатора магнитный поток. При возникновении токов утечки изменяется значение токов, которые проходят через трансформатор. В данном случае происходит срабатывание реле. Работа УЗО прекращается благодаря наличию реле, которое запускает присутствующий пружинный механизм.
- 1) Корпус, созданный из пластика.

- 2) Замок для подсоединения к ДИН-рейке.
- 3) Трансформатор тока.
- 4) Электромагнитное реле.
- 5) Расцепитель тока.
- 6) Дугогасительные камеры.
- 7) Медные клеммы.
Напишите нам чтобы начать сотрудничество
* Поля обязательные для заполнения
Как работают дифференциалы | HowStuffWorks
Если вы читали «Как работают автомобильные двигатели», вы понимаете, как генерируется мощность автомобиля; и если вы читали книгу «Как работают механические коробки передач», вы понимаете, куда дальше уходит мощность. В этой статье будет рассказано о дифференциалах , где мощность в большинстве автомобилей делает свою последнюю остановку перед тем, как пробуксовывать колеса.
Дифференциал выполняет три функции:
- Направляет мощность двигателя на колеса
- Работает в качестве конечной понижающей передачи в автомобиле, замедляя скорость вращения трансмиссии в последний раз перед тем, как она ударит по колесам
- Для передавать мощность на колеса, позволяя им вращаться с разной скоростью (именно благодаря этому дифференциал получил свое название).
 )
)
В этой статье вы узнаете, зачем вашему автомобилю нужен дифференциал, как он работает и в чем его недостатки. Мы также рассмотрим несколько типов позиционной тяги, также известных как дифференциалы повышенного трения .
Зачем нужен дифференциал
Колеса автомобиля крутятся с разной скоростью, особенно при поворотах. Вы можете видеть из анимации, что каждое колесо проходит разное расстояние за поворот, и что внутренние колеса проходят меньшее расстояние, чем внешние колеса.Поскольку скорость равна пройденному расстоянию, деленному на время, затрачиваемое на это расстояние, колеса, преодолевающие меньшее расстояние, движутся с меньшей скоростью. Также обратите внимание, что передние колеса проходят другое расстояние, чем задние колеса.
Для неприводных колес на вашем автомобиле — передние колеса на заднеприводном автомобиле, задние колеса на переднеприводном автомобиле — это не проблема. Между ними нет связи, поэтому они вращаются независимо. Но ведущие колеса соединены вместе, так что один двигатель и трансмиссия могут вращать оба колеса.Если бы в вашей машине не было дифференциала, колеса пришлось бы сблокировать вместе, заставив вращаться с одинаковой скоростью. Это затруднило бы поворот автомобиля: чтобы автомобиль мог поворачивать, одна шина должна проскальзывать. С современными шинами и бетонными дорогами требуется большое усилие, чтобы заставить шину пробуксовывать. Эта сила должна была бы передаваться через ось от одного колеса к другому, создавая большую нагрузку на компоненты оси.
Но ведущие колеса соединены вместе, так что один двигатель и трансмиссия могут вращать оба колеса.Если бы в вашей машине не было дифференциала, колеса пришлось бы сблокировать вместе, заставив вращаться с одинаковой скоростью. Это затруднило бы поворот автомобиля: чтобы автомобиль мог поворачивать, одна шина должна проскальзывать. С современными шинами и бетонными дорогами требуется большое усилие, чтобы заставить шину пробуксовывать. Эта сила должна была бы передаваться через ось от одного колеса к другому, создавая большую нагрузку на компоненты оси.
Дифференциальная машина — История Чарльза Бэббиджа Дифференциальная машина
Чарльз Бэббидж, 1791-1871.Портрет из журнала Illustrated London News , 4 ноября 1871 года
Числовая таблица — это инструмент, предназначенный для экономии времени и труда тех, кто занимается вычислительной работой. Самые старые таблицы, которые сохранились, были составлены в Вавилоне в период 1800-1500 гг. до н.э. Они предназначались для преобразования единиц, для умножения и деления и были начертаны клинописью на кусочках глины. В течение первого века до н.э. Клавдий Птолемей в Александрии создал свою теорию движения небесных тел в труде, который позже стал известен под названием Альмагест
В течение первого века до н.э. Клавдий Птолемей в Александрии создал свою теорию движения небесных тел в труде, который позже стал известен под названием Альмагест
Они должны были составить один из самых важных астрономических документов Древнего мира, и они содержали все необходимые таблицы для расчета затмений, а также различного рода эфемерид, т. е. таблицы, в которых указывалось положение небесных тел в определенный период, т. е.г. каждый день в течение всего года. В первой половине тринадцатого века таблицы Птолемея привлекли внимание короля Кастилии Альфонсо Мудрого. Затем он собрал большое количество ученых в Толедо, которым было поручено составить новую коллекцию астрономических таблиц. Говорят, что причиной этого усилия было то, что король Альфонсо, который интересовался астрономией, обнаружил много ошибок в таблицах Птолемея. Работа началась где-то в 1240-х годах и заняла около десяти лет.Произведенные столы позже были известны как Alphonsine Tables . Огромные затраты были оплачены королем, чье имя вскоре распространилось вместе с копиями таблиц по всему европейскому научному миру. Помимо вавилонских таблиц, работы Птолемея и таблиц Альфонса, в этот период много труда было потрачено на создание многих других числовых таблиц различного рода.
Огромные затраты были оплачены королем, чье имя вскоре распространилось вместе с копиями таблиц по всему европейскому научному миру. Помимо вавилонских таблиц, работы Птолемея и таблиц Альфонса, в этот период много труда было потрачено на создание многих других числовых таблиц различного рода.
С распространением книгопечатания по всей Европе во второй половине 15 века были напечатаны первые таблицы.Таблицы Альфонсов, например, были напечатаны в Венеции в 1483 году. В конце шестнадцатого века было опубликовано несколько известных арифметических и тригонометрических таблиц. Для того, чтобы упростить работу по умножению, были опубликованы таблицы умножения. Настоящая революция в бизнесе с таблицами произошла после открытия Джоном Нейпиром логарифмов в 1614 году. Имея под рукой таблицу логарифмов, вычислительные усилия можно было значительно сократить. В 1617 году Генри Бриггс опубликовал первую таблицу логарифмов.
Двести лет спустя, в начале 19-го века, числовые таблицы по-прежнему были самым важным вспомогательным средством для расчетов в Европе. Единственными альтернативами были кости Нейпира и логарифмическая линейка. Механические счетные машины были чрезвычайно редки, и самое большее горстка очень избранных людей могла когда-либо использовать их для серьезных вычислений. Большинство из них были просто замечательными приспособлениями, иллюстрирующими научный прогресс человека, а не подлинными помощниками в расчетах. Для обычного калькулятора или ученого, которому приходилось выполнять сложные вычисления, требующие большой точности, стержни Непера и логарифмическая линейка мало чем могли помочь.По сути, его инструментами были ручка, бумага и таблицы. Были таблицы по математике, астрономии, навигации, физике, технике, статистике, торговле и финансам, в армии и во многих других областях. Однако публикация таких таблиц требовала большого количества ручной расчетной работы, а конечный продукт был полон ошибок.
Единственными альтернативами были кости Нейпира и логарифмическая линейка. Механические счетные машины были чрезвычайно редки, и самое большее горстка очень избранных людей могла когда-либо использовать их для серьезных вычислений. Большинство из них были просто замечательными приспособлениями, иллюстрирующими научный прогресс человека, а не подлинными помощниками в расчетах. Для обычного калькулятора или ученого, которому приходилось выполнять сложные вычисления, требующие большой точности, стержни Непера и логарифмическая линейка мало чем могли помочь.По сути, его инструментами были ручка, бумага и таблицы. Были таблицы по математике, астрономии, навигации, физике, технике, статистике, торговле и финансам, в армии и во многих других областях. Однако публикация таких таблиц требовала большого количества ручной расчетной работы, а конечный продукт был полон ошибок.
Где-то в 1821 году молодому английскому математику Чарльзу Бэббиджу (биография Чарльза Бэббиджа) пришла в голову идея о механических вычислениях. Он предоставил нам две версии происхождения своих представлений о машинах, но одна, написанная в 1822 году, кажется более правдоподобной, чем другая, появившаяся в его автобиографии сорок лет спустя.
Он предоставил нам две версии происхождения своих представлений о машинах, но одна, написанная в 1822 году, кажется более правдоподобной, чем другая, появившаяся в его автобиографии сорок лет спустя.
Согласно первому рассказу, в 1820 или 1821 году Астрономическое общество поручило Бэббиджу и его другу Гершелю одно из заданий по улучшению таблиц навигационной книги Морской альманах . Они построили соответствующие формулы и поручили арифметику клеркам. Чтобы уменьшить количество ошибок, расчеты выполнялись дважды, каждый раз другим клерком. Затем они сравнили два набора на наличие расхождений. В ходе утомительной проверки Гершель и Бэббидж обнаружили ряд ошибок, и в какой-то момент Бэббидж сказал: Я желаю, чтобы эти вычисления были выполнены паром . Вполне возможно , заметил Гершель.
Но в своей автобиографии Бэббидж вспомнил другую версию этой истории, которая, должно быть, произошла то ли в 1812, то ли в 1813 году:
«…Я сидел в помещении Аналитического общества, в Кембридже, склонив голову вперед на стол в виде мечтательного настроения, с открытой передо мной таблицей логарифмов. Другой участник, войдя в комнату и увидев меня в полусне, крикнул: «Ну, Бэббидж, о чем ты мечтаешь?» на что я ответил: «Я думаю, что все эти таблицы» (указывая на логарифмы) «могут быть рассчитаны с помощью машин.
Другой участник, войдя в комнату и увидев меня в полусне, крикнул: «Ну, Бэббидж, о чем ты мечтаешь?» на что я ответил: «Я думаю, что все эти таблицы» (указывая на логарифмы) «могут быть рассчитаны с помощью машин.
Как бы то ни было, где-то в 1820 или 1821 году Бэббидж начал свою работу над вычислительной машиной, создав несколько конструкций часовых механизмов, которые можно было заставить управлять набором колес с числами по краям, которые можно было печатать на бумага. Он сделал небольшую модель, состоящую из 96 колес и 24 осей, которую позже уменьшил до 18 колес и 3 осей. Машина была готова к концу весны 1822 года, а в июне о ней было объявлено публично, и ее осмотрели несколько членов Астрономического общества.
Кажется, Бэббидж, должно быть, очень мало знал о конструкции машин, механических вычислениях и истории таких машин в то время, потому что он начал с рассмотрения использования скользящих стержней вместо более естественного использования колес в счетном механизме. Этот вид механизма, который был «новым» в истории счетных машин, порождает серьезные трудности в процессе переноски, что в конце концов осознал Бэббидж. На самом деле это, кажется, было для него таким откровением, что в ноябре 1822 года он очень торжественно отметил, что в будущем решил всегда выбирать для этой цели круговое движение.
Этот вид механизма, который был «новым» в истории счетных машин, порождает серьезные трудности в процессе переноски, что в конце концов осознал Бэббидж. На самом деле это, кажется, было для него таким откровением, что в ноябре 1822 года он очень торжественно отметил, что в будущем решил всегда выбирать для этой цели круговое движение.
Рабочая модель имела секцию вычислительного механизма, включающую два порядка разницы, но не печатающего механизма. Он успешно вычислил первые тридцать значений, вытекающих из формулы + x + 41 , которая была его любимым примером, потому что она генерирует много простых чисел. Машина выдавала правильные результаты со скоростью 33 цифры в минуту, поэтому значения были сведены в таблицу за две с половиной минуты. Позже в том же году Бэббидж написал записку в Общество и статью «О теоретических принципах машин для расчета таблиц» для Brewster’s Journal of Science:
. порядок определяется расчетом.Механизмы таковы, что… не должно существовать возможности ошибки в любой печатной копии таблиц, вычисленных этой машиной.
Бэббидж также написал письмо на общую тему президенту Королевского общества сэру Хамфри Дэви. В этом письме Бэббидж указал на преимущества такой машины для правительства в производстве длинных таблиц для навигации и астрономии и предложил построить машину в увеличенном масштабе для использования правительством.
Астрономическое общество восприняло предложение Бэббиджа с большим энтузиазмом, а Королевское общество положительно отозвалось о его проекте создания того, что он назвал Разностной машиной , специализированной вычислительной машины для расчета таблиц с использованием метода разностей
Бэббидж был не первым, кто предложил печатный калькулятор, и не первым, кто предложил метод разностей в качестве подходящего принципа, на котором можно было бы основывать механизированные вычисления.Это отличие принадлежит немецкому инженеру и мастеру-строителю Иоганну Гельфриху Мюллеру, который еще в 1784 году описал свои мечты о счетной машине, основанной на методе разностей, но его идея осталась только на бумаге. Есть сведения, что в какой-то момент Бэббидж узнал о Мюллере и его проекте, но произошло это, скорее всего, после 1821 года, когда он уже начал работу над Разностной машиной
Есть сведения, что в какой-то момент Бэббидж узнал о Мюллере и его проекте, но произошло это, скорее всего, после 1821 года, когда он уже начал работу над Разностной машиной
 Возьмите второе различие и добавьте его к первому различию, чтобы сформировать новое первое различие, 4+2=6. Процесс можно обобщить. В нашем примере вторая разность постоянна, поскольку функция T является квадратичной. Если бы функция T была кубической, такой как T = x , то вторая разность изменялась бы, но третья разность, разность между последовательными вторыми разностями, была бы постоянной.В общем случае многочлен степени будет иметь постоянную разность n th , и каждое последующее новое значение функции может быть получено n простыми сложениями.
Возьмите второе различие и добавьте его к первому различию, чтобы сформировать новое первое различие, 4+2=6. Процесс можно обобщить. В нашем примере вторая разность постоянна, поскольку функция T является квадратичной. Если бы функция T была кубической, такой как T = x , то вторая разность изменялась бы, но третья разность, разность между последовательными вторыми разностями, была бы постоянной.В общем случае многочлен степени будет иметь постоянную разность n th , и каждое последующее новое значение функции может быть получено n простыми сложениями. Полезность разностных методов значительно повышается благодаря тому факту, что любой участок хорошо функционирующей непрерывной функции может быть аппроксимирован многочленом. Чем короче участок и чем выше степень многочлена, тем ближе аппроксимация. Поэтому, если мы хотим свести в таблицу функцию, такую как синус или время заката, необходимо только разделить функцию на достаточно короткие интервалы и найти подходящий аппроксимирующий многочлен для каждого интервала.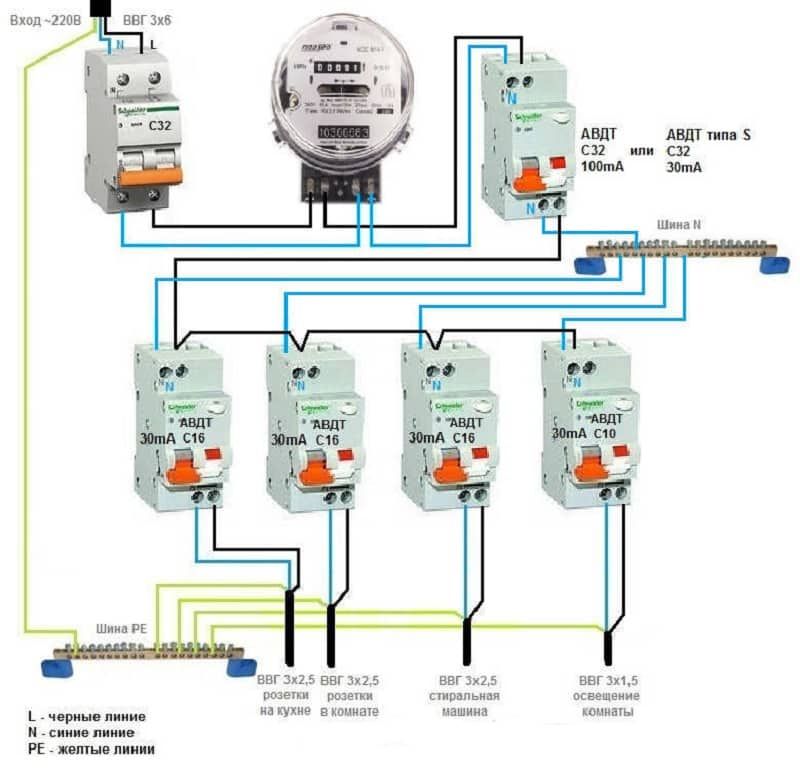 Затем можно использовать метод разностей для табулирования функции на протяжении всего интервала. Этот процесс известен как подтаблица. Бэббидж понял, что машина может выполнять этот процесс составления подтаблиц. Во-первых, ему нужен был механизм хранения отдельно чисел, соответствующих значениям табличного значения, первой разности, второй разности и т. д. и механизм добавления каждой разности к значению предыдущей разности.
Затем можно использовать метод разностей для табулирования функции на протяжении всего интервала. Этот процесс известен как подтаблица. Бэббидж понял, что машина может выполнять этот процесс составления подтаблиц. Во-первых, ему нужен был механизм хранения отдельно чисел, соответствующих значениям табличного значения, первой разности, второй разности и т. д. и механизм добавления каждой разности к значению предыдущей разности.
В процессе проектирования и сборки своей разностной машины Бэббиджу потребовалось много точных чертежей деталей.При использовании этих чертежей он чувствовал, что они не полностью и адекватно описывают механизм. Для машины со многими частями, движущимися по-разному, статические чертежи могли показать только форму и расположение частей. Поэтому Чарльз разработал систему механических обозначений, которая также указывала бы, как двигаются части — их скорости и взаимосвязи. В отличие от обычных рисунков, в обозначениях не изображались формы деталей. Скорее это была таблица чисел, строк и символов для описания действий машины. Это была общая система, которую можно было использовать для описания любой машины. Чарльз опубликовал описание своей механической записи в Philosophical Transactions of the Royal Society в 1826 году, а затем в 1851 году (см. Законы механической записи). Однако эта механическая запись так и не получила широкого распространения.
Это была общая система, которую можно было использовать для описания любой машины. Чарльз опубликовал описание своей механической записи в Philosophical Transactions of the Royal Society в 1826 году, а затем в 1851 году (см. Законы механической записи). Однако эта механическая запись так и не получила широкого распространения.
В интервью, состоявшемся в 1823 году между Бэббиджем и канцлером казначейства, было достигнуто довольно расплывчатое устное соглашение, в соответствии с которым правительство предоставит средства для предприятия, которое, как предполагалось, займет три года.Его собственное астрономическое общество было настолько впечатлено этой машиной, что наградило его первой золотой медалью в 1824 году. В том же году британское правительство выделило Бэббиджу гонорар в размере 1500 фунтов стерлингов, и он начал конструировать полную разностную машину . Бэббидж нуждался в небольшой фабрике и грамотных рабочих, хотя изначально две комнаты в доме Бэббиджа были превращены в мастерские, а третья в кузницу. Он нанял хорошего инженера — Джозефа Клемента, чтобы тот обслуживал механические работы в его мастерской. К 1828 году Чарльз потратил на строительство более 6000 фунтов стерлингов, а правительство возместило ему только 1500 фунтов стерлингов.После благосклонного отчета друзей Чарльза из Королевского общества правительство согласилось компенсировать разницу. Но работа шла довольно медленно.
Он нанял хорошего инженера — Джозефа Клемента, чтобы тот обслуживал механические работы в его мастерской. К 1828 году Чарльз потратил на строительство более 6000 фунтов стерлингов, а правительство возместило ему только 1500 фунтов стерлингов.После благосклонного отчета друзей Чарльза из Королевского общества правительство согласилось компенсировать разницу. Но работа шла довольно медленно.
Весь проект занял гораздо больше времени, чем кто-либо ожидал. Пока шло изготовление основных деталей, нужно было нарисовать цеховые выкройки для других. Полный набор планов не был завершен до 1830 года. К тому времени рабочие Клемента изготовили многие тысячи деталей, но почти не занимались сборкой.
Вскоре Бэббидж и правительство решили, что чертежи и сборку следует вынести из мастерской Клемента.На территории Бэббиджа была построена двухэтажная противопожарная мастерская и второе здание для Разностной машины. Намерение Бэббиджа состояло в том, чтобы перенести все операции Клемента в эти новые помещения. Однако Клемент сопротивлялся, потому что на средства, предоставленные ему Бэббиджем, он значительно расширил свою собственную мастерскую. Теперь у него было много станков и несколько служащих, и он использовал их для выполнения другой работы, помимо той, которую нанял Бэббидж. И, согласно торговой практике того времени, он настаивал на том, что оборудование принадлежит ему, а не Бэббиджу или правительству.
Однако Клемент сопротивлялся, потому что на средства, предоставленные ему Бэббиджем, он значительно расширил свою собственную мастерскую. Теперь у него было много станков и несколько служащих, и он использовал их для выполнения другой работы, помимо той, которую нанял Бэббидж. И, согласно торговой практике того времени, он настаивал на том, что оборудование принадлежит ему, а не Бэббиджу или правительству.
В течение 1832 года рабочие Клемента завершили сборку двигателя в количестве, для которого у них было деталей (было изготовлено около 10000 деталей). Несмотря на то, что расчетная секция была в основном завершена, а секция печати — нет. С этого времени дальнейшая работа не велась. Клемент не стал переносить свое оборудование в мастерскую Бэббиджа, и только в 1834 году был передан сам двигатель. К тому времени правительство израсходовало 17000 фунтов стерлингов, а Бэббидж потратил около шести тысяч фунтов собственных денег. Правительство не желало двигаться дальше, учитывая необходимость реорганизации всего проекта после того, как Клемент и Бэббидж расстались.
Почти все части всего счетного механизма были изготовлены, но не собраны, когда работа над проектом была остановлена в начале 1833 г. Часть счетного механизма была собрана в 1832 г. (см. нижнее фото) для демонстрации комитету. Королевского общества и парламента, что проект осуществляется удовлетворительно, но он был ограничен двумя порядками разности и пятью цифрами, подходящими только для демонстрационных целей.
Он составляет примерно одну треть высоты и половину ширины, или примерно одну седьмую часть всего счетного механизма и состоит примерно из 2000 бронзовых и стальных деталей.Одна только вычислительная часть была бы в 7 раз больше, чем маленький блок, который был собран. Предполагалось, что вся машина будет содержать около 25000 деталей и весить более 2 тонн, а ее размеры будут примерно 260 см в высоту, 230 см в ширину и 100 см в глубину.
Часть разностной машины, собранная в 1832 году
Конструкция разностной машины
Разностная машина состояла из двух основных частей — вычислительного механизма и механизма печати и управления. На нижнем чертеже 1830 г. фасада (верхняя часть рисунка) и чертежах плана (нижняя часть) Разностной машины они хорошо видны. Счетный механизм слева, хорошо видны оси фигурных колес для табличного значения (крайний справа) и шесть разностей. Печатный механизм находится справа, а в центре обоих рисунков виден подвижный стол со стереотипной печатной формой и сектор с пуансонами цифрового типа.
На нижнем чертеже 1830 г. фасада (верхняя часть рисунка) и чертежах плана (нижняя часть) Разностной машины они хорошо видны. Счетный механизм слева, хорошо видны оси фигурных колес для табличного значения (крайний справа) и шесть разностей. Печатный механизм находится справа, а в центре обоих рисунков виден подвижный стол со стереотипной печатной формой и сектор с пуансонами цифрового типа.
Фасад (верхняя часть рисунка) и чертежи в плане Разностной Машины, начиная с 1830 г.
Цифры представлены в Разностной Машине положением вращения горизонтальных зубчатых колес.Число состоит из ряда этих фигурных колес, вращающихся вокруг общей вертикальной оси. Самое нижнее колесо представляет единицы, следующие десятки, следующие сотни и так далее. Фигурные колеса имеют диаметр около 15 сантиметров и расположены вертикально на расстоянии около 7,5 сантиметров друг от друга по осям. Бэббидж использовал термин , ось , чтобы обозначить стопку фигурных колес, которые вместе хранят число как набор десятичных цифр. Вся разностная машина состоит из оси для табличного значения функции, другой оси для разности, третьей оси для второй разности и т. д. для стольких порядков разностей, сколько требуется.
Вся разностная машина состоит из оси для табличного значения функции, другой оси для разности, третьей оси для второй разности и т. д. для стольких порядков разностей, сколько требуется.
Часть разностной машины (с обложки Отрывки из жизни философа , 1864)
Каждая ось служила не только хранилищем чисел, но и счетным механизмом. Добавление происходило в два этапа, которые будут объяснены со ссылкой на добавление первой разницы к табличному значению. Внутри каждого фигурного колеса первой разности есть механизм, который вращается на столько же шагов, сколько значение хранит числовое колесо. Если числовое колесо единиц равно 3, то механизм будет двигаться через три шага.Это движение передается посредством зубчатой передачи на соответствующее числовое колесо оси табличных значений. Если последний первоначально был равен 5, то он переместится на три шага и станет равным 8. Этот процесс происходит одновременно в десятках, сотнях, тысячах и других позициях разряда.
Может случиться так, что добавление к цифровому колесу приведет к переносу, который необходимо распространить на следующую более высокую цифровую позицию. Если цифра единиц табличного значения изначально была 6, а к ней добавлено 7, она переместится вперед на семь позиций и станет на три, но перенос также должен быть распространен на колесо десятков табличного значения.Распространение переноса усложняется тем фактом, что если колесо десятков уже стоит на 9, оно будет перемещено переносом вперед, чтобы стоять на 0, и новый перенос будет распространяться на колесо цифр сотен. В разностной машине эти последовательные переносы могут распространяться, как иногда и должно быть, от единиц вверх по наиболее значимому цифровому колесу. Таким образом, каждое добавление состоит из двух отдельных шагов: одновременного добавления всех цифр первой разности к соответствующим цифрам табличного значения и последовательного распространения переносов от единиц до старших значащих цифр по мере необходимости.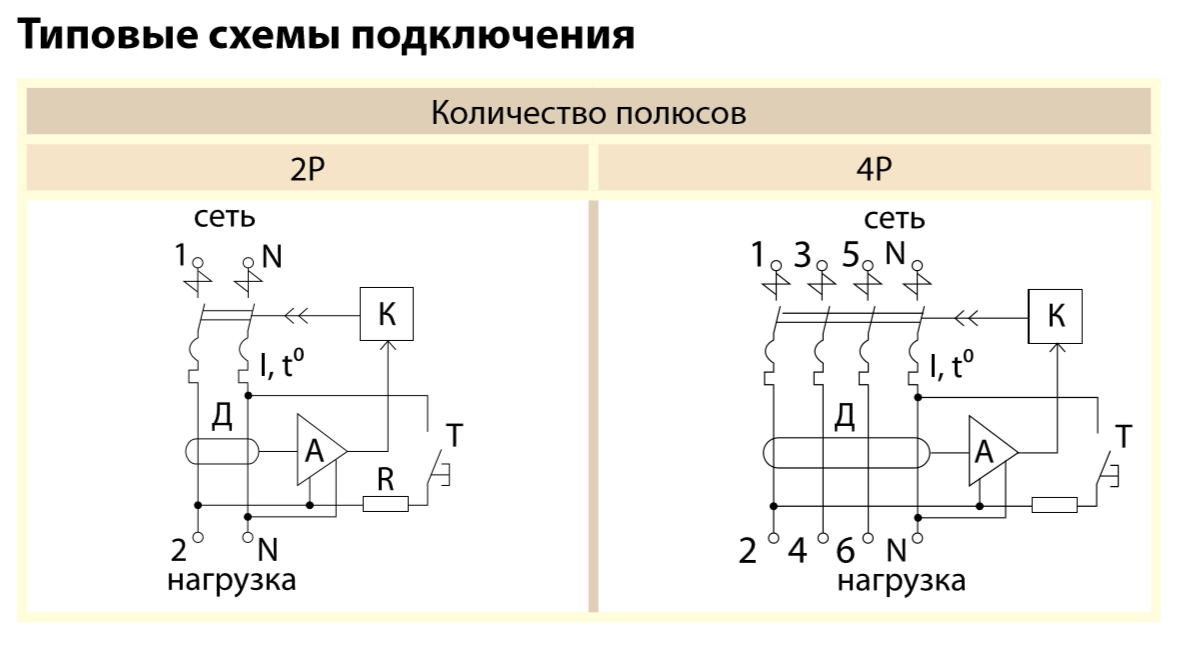
1. Добавление цифр третьей разности к цифре второй разности
2 , Распространение переноса среди цифр второй разности
3. Вторая разность добавляется к первой разнице
4.Распространение переноса среди первых цифр разности
5. Первая разность добавляется в столбец результатов
6. Перенос имел место в столбце результатов
Отрицательные числа можно обрабатывать без дополнительного механизма, представляя их как их дополнения до десятков.
Эта схема легко распространяется на разности более высокого порядка. Очевидно, что количество шагов равно удвоенному количеству мощности функции, а это значит, что для функций большей мощности потребуется много шагов. Бэббидж нашел способ перестроить расчет так, чтобы для каждого полученного табличного значения требовалось всего четыре шага, независимо от количества задействованных различий. Это характерно для изощренных логических соображений, лежащих в основе замыслов Бэббиджа.
Бэббидж нашел способ перестроить расчет так, чтобы для каждого полученного табличного значения требовалось всего четыре шага, независимо от количества задействованных различий. Это характерно для изощренных логических соображений, лежащих в основе замыслов Бэббиджа.
Бэббидж заметил, что когда к табличному значению прибавляется первая разность, на шагах пять и шесть обе оси разности — третья и вторая — простаивают. Таким образом, он мог бы добавить третью разность ко второй разнице, шаги один и два, в то же самое время, когда первая разность добавляется к табличному значению.Шаги один и два пересекаются с шагами пять и шесть. Таким образом, для каждого полученного табличного значения требуется всего четыре единицы времени для шагов с третьего по шестой. Используя современную терминологию, мы бы назвали такое расположение оборудования для выполнения вычислений конвейером
. Идея перекрытия может быть расширена до более высоких разностей, и новое табличное значение всегда может быть получено в четыре этапа, а именно:
1. Нечетное разности добавляются к четным и к результату.
Нечетное разности добавляются к четным и к результату.
2. Перенос происходит в четных различиях и в результате.
3. К нечетным прибавляются четные различия.
4. Переноска происходит в нечетных разностях.
Эта измененная форма вычислений не только экономит значительное время, но и значительно упрощает организацию механизма вычислений.
Похоже, что Чарльз Бэббидж изначально не определил математическую мощность двигателя. Он только описывает его как предназначенный для более крупного двигателя . В 1823 году машина была сделана для расчета с четырьмя порядками разностей.Количество цифр не указано. В 1829 году сообщалось, что машина может работать с разностями шестого порядка, 12 цифрами и печатать 16 цифр в результате со скоростью сорок четыре цифры в минуту. В какой-то момент Бэббидж согласился на шесть порядков разностей, но количество цифр продолжало варьироваться в зависимости от автора. 18 цифр упоминаются в 1834 году, и сам Бэббидж, будучи стариком, сказал, что вся машина была бы способна выполнять вычисления с 20 разрядами цифр.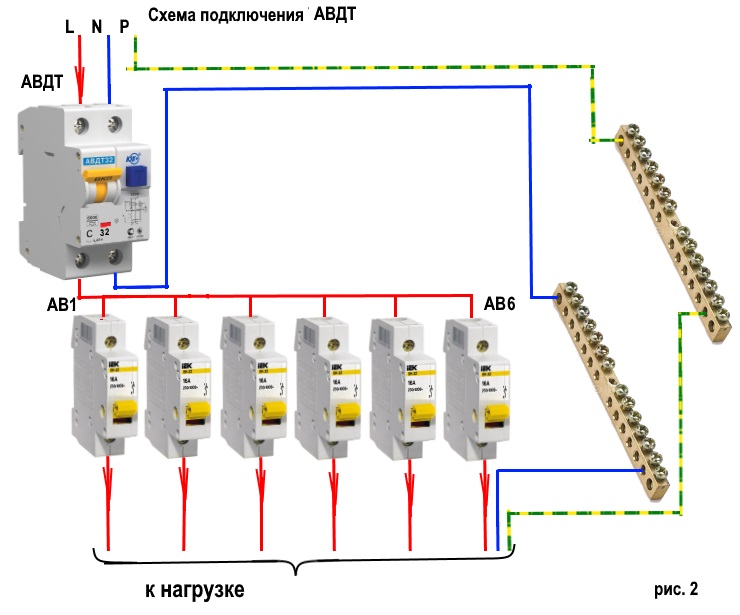
Очень жаль, что работа над Разностной Машиной остановилась так близко к завершению. Позже Генри Бэббидж подсчитал, что хватило бы еще только пятисот фунтов. Бэббидж мог легко найти средства, однако его чувства и отношение как к правительству, так и к Клементу не могли позволить ему сделать это.Кроме того, в течение года или двух мысли Бэббиджа продвинулись далеко вперед в направлении гораздо более сложной и интеллектуально полезной аналитической машины. Тогда он никак не мог вернуться к первоначальной конструкции разностной машины и довести ее до конца, даже если бы события сделали это возможным.
В конце 1860-х годов Бэббидж сказал: «Я не закончил ее [разностную машину], потому что, работая над ней, я пришел к идее моей аналитической машины, которая делала бы все, на что она была способна, и даже больше. На самом деле идея была настолько проще, что для завершения вычислительной машины потребовалось бы больше работы, чем для разработки и создания другой целиком, поэтому я обратил свое внимание на аналитическую машину».
На самом деле идея была настолько проще, что для завершения вычислительной машины потребовалось бы больше работы, чем для разработки и создания другой целиком, поэтому я обратил свое внимание на аналитическую машину».
Тем не менее не подлежит сомнению, что Разностная Машина стояла как великий памятник человеческой изобретательности и способности механизировать все виды труда. Идея была слишком важной и захватывающей, чтобы ее можно было забыть. Усилия Бэббиджа вызвали широкую огласку, что было важным фактором в сохранении идеи.Другим фактором, естественно, была сама проблема. Горстка изобретателей, все с разным опытом, должны были попытаться в течение 19 века построить разностные двигатели в соответствии со своими собственными идеями. Первым из них был швед Пер Георг Шойц, которому лишь небольшой частью ресурсов Бэббиджа удалось в середине 19 века изготовить работающий разностный двигатель.
В течение нескольких лет Бэббидж демонстрировал рабочую часть своей разностной машины в одной из своих гостиных и использовал часть вычислительного механизма для вычисления почти сотни функций. Он даже разработал некоторые усовершенствования оригинального механизма. В разностной машине всякий раз, когда в наборе вычислений требовалась новая константа, ее нужно было вводить вручную. В 1834 году Бэббидж придумал способ вставлять различия механически, располагая оси разностной машины по кругу так, чтобы столбец «Результат» находился рядом со столбцом последней разности и, таким образом, был легко доступен для нее. Он назвал эту схему двигатель, поедающий собственный хвост . Но это вскоре привело к идее управлять машиной совершенно независимыми средствами и заставить ее выполнять не только сложение, но и все арифметические процессы по желанию в любом порядке и столько раз, сколько может потребоваться.Работа над первой разностной машиной была остановлена 10 апреля 1833 года, а первый чертеж аналитической машины датирован сентябрем 1834 года. разработка разностной машины № 2, использующая улучшенные и упрощенные арифметические механизмы, разработанные для аналитической машины.
Он даже разработал некоторые усовершенствования оригинального механизма. В разностной машине всякий раз, когда в наборе вычислений требовалась новая константа, ее нужно было вводить вручную. В 1834 году Бэббидж придумал способ вставлять различия механически, располагая оси разностной машины по кругу так, чтобы столбец «Результат» находился рядом со столбцом последней разности и, таким образом, был легко доступен для нее. Он назвал эту схему двигатель, поедающий собственный хвост . Но это вскоре привело к идее управлять машиной совершенно независимыми средствами и заставить ее выполнять не только сложение, но и все арифметические процессы по желанию в любом порядке и столько раз, сколько может потребоваться.Работа над первой разностной машиной была остановлена 10 апреля 1833 года, а первый чертеж аналитической машины датирован сентябрем 1834 года. разработка разностной машины № 2, использующая улучшенные и упрощенные арифметические механизмы, разработанные для аналитической машины. Логический дизайн был таким же, как и у более ранней разностной машины, но он использовал более простые механизмы для хранения и добавления чисел и распространения переноса.Механизм печати был упрощен, так что целое число печаталось на печатной форме за одно действие, а не поразрядно. Одновременно была сделана обычная печатная копия с использованием красящих валиков. Управление было организовано одним стволом очень просто. К середине 1848 года был подготовлен проект и полный комплект чертежей. Они были предложены Бэббиджем британскому правительству, по-видимому, для выполнения обязательства, которое, по его мнению, существовало вследствие провала проекта по созданию первой разностной машины, но правительство не проявляет интереса к новой конструкции.
Логический дизайн был таким же, как и у более ранней разностной машины, но он использовал более простые механизмы для хранения и добавления чисел и распространения переноса.Механизм печати был упрощен, так что целое число печаталось на печатной форме за одно действие, а не поразрядно. Одновременно была сделана обычная печатная копия с использованием красящих валиков. Управление было организовано одним стволом очень просто. К середине 1848 года был подготовлен проект и полный комплект чертежей. Они были предложены Бэббиджем британскому правительству, по-видимому, для выполнения обязательства, которое, по его мнению, существовало вследствие провала проекта по созданию первой разностной машины, но правительство не проявляет интереса к новой конструкции.
 Позже Генри хорошо разобрался в конструкции разностной (и аналитической) машины и установил тесную связь со своим отцом, которого он навещал в отпуске после продолжительной военной службы в Индии.Бэббидж завещал свои чертежи, мастерскую и уцелевшие физические реликвии двигателей Генри, который пытался продолжить дело своего отца и предать гласности двигатели после смерти Бэббиджа.
Позже Генри хорошо разобрался в конструкции разностной (и аналитической) машины и установил тесную связь со своим отцом, которого он навещал в отпуске после продолжительной военной службы в Индии.Бэббидж завещал свои чертежи, мастерскую и уцелевшие физические реликвии двигателей Генри, который пытался продолжить дело своего отца и предать гласности двигатели после смерти Бэббиджа.Генри был у постели своего отца, когда Бэббидж умер 18 октября 1871 года, а с 1872 года он усердно продолжал работу своего отца, а затем периодически уходил на пенсию в 1875 году. он отправил в Гарвард. В 1930-х годах эта работа привлекла внимание Говарда Эйкена, создателя Harvard Mark I, калькулятора с программным управлением.
Верь только половине того, что видишь, и ничему, что слышишь.
Эдгар Аллан По
Какая разница, которую создал двигатель: из калькулятора Чарльза Бэббиджа появился современный компьютер | История
Как можно догадаться из названия, «Разностная машина» — очень сложный для описания объект. Вы можете начать с того, что вообразите боковую часть большой кроватки со стойками, окруженными маленькими металлическими колесами — или, скорее, катушками, — но лучше увидеть это своими глазами.
Вы можете начать с того, что вообразите боковую часть большой кроватки со стойками, окруженными маленькими металлическими колесами — или, скорее, катушками, — но лучше увидеть это своими глазами.
Хорошо очищенный от пыли и с отполированной латунной фурнитурой он выставлен в первой галерее выставки «Век информации» в Национальном музее американской истории. Хотя усиленный голос указывает на важность машины в истории науки, он редко собирает толпу. Не сомневайтесь, однако, в том, что разностная машина является звеном мощного интеллектуального возбуждения и удивительного человека, которого британское правительство недавно удостоило собственной почтовой маркой. Это Чарльз Бэббидж, человек, который более 150 лет назад впервые слабо увидел сегодняшний компьютерный век и стремился достичь его.
Разностная машина — это калькулятор. Он готовит числовые таблицы с использованием математической техники, известной как метод разницы. Сегодня такие таблицы — такие, которые часто используются в навигации и астрономии, — будут вычисляться и храниться в электронном виде. Почти полтора века назад разностная машина выполняла почти ту же работу, но медленно и механически.
Почти полтора века назад разностная машина выполняла почти ту же работу, но медленно и механически.
Двое шведов, Георг Шойц и его сын Эдвард, построили Смитсоновскую машину в 1853 году. Каждый из ее длинных валов удерживает диски, и каждый диск имеет колеса с десятью зубьями, которые соответствуют отметкам на дисках.Ученый мог установить диски с известными числами, нечетными или четными, повернуть рукоятку и, считывая показания каждого вала, найти результат вычисления. Этот конкретный «двигатель» также может распечатывать свои ответы. Проданный обсерватории в Олбани, штат Нью-Йорк, он был передан Смитсоновскому институту в 1963 году.
Шойцев не интересовал приятный дизайн. Однако их устройство работало хорошо, поскольку они довели до практического завершения концепцию одного из самых блестящих умов XIX века.Изобретатель и философ, Бэббидж создал прототип оригинальной разностной машины еще в 1822 году, а затем продолжал вносить усовершенствования, так и не закончив ее. Он с энтузиазмом поддержал работу своих друзей Георга и Эдварда Шойц. Но в течение многих лет, которые ушли на создание их машины, изобретатель нащупывал механическое устройство, которое вышло бы далеко за рамки расчетов. На самом деле он будет хранить данные, которые он произвел, а затем повторно использовать информацию, чтобы добавить больше.Бэббидж описал этот процесс как «двигатель, пожирающий собственный хвост».
Он с энтузиазмом поддержал работу своих друзей Георга и Эдварда Шойц. Но в течение многих лет, которые ушли на создание их машины, изобретатель нащупывал механическое устройство, которое вышло бы далеко за рамки расчетов. На самом деле он будет хранить данные, которые он произвел, а затем повторно использовать информацию, чтобы добавить больше.Бэббидж описал этот процесс как «двигатель, пожирающий собственный хвост».
То, что он предвидел, было примитивным компьютером. Как писал его биограф Энтони Хайман: «Бэббидж работал в одиночку, намного опережая современные мысли. Ему приходилось не только разрабатывать проекты, но и разрабатывать концепции, инженерные решения и даже инструменты для изготовления деталей. … стоит особняком: великая предковая фигура вычислительной техники».
Чарльз Бэббидж родился в 1791 году в богатой и праздной семье Девоншира.Он пошел в хорошую школу, а затем отправился в Кембридж, почти не представляя себе, чего там ожидать, за исключением предупреждения, что это плохое место для покупки вина. Блестящий по математике от природы, он обнаружил, что его профессора математики на самом деле знают меньше, чем он.
Блестящий по математике от природы, он обнаружил, что его профессора математики на самом деле знают меньше, чем он.
Явный гений, Чарльз, кажется, также был очаровательным молодым человеком, полным юношеской решимости улучшить преподавание математики в Кембридже. Вместе со своим близким другом Джоном Гершелем, сыном знаменитого астронома Уильяма Гершеля, Бэббидж помог основать Аналитическое общество.
Подобно Лунному обществу во времена Иосии Веджвуда и Эразма Дарвина (дедушки Чарльза), двумя поколениями ранее, «Аналитики» собирались в шумной компании для обсуждения, среди прочего, производства ткани из хлопка и шерсти и железные кузницы и сталелитейные заводы, заполнявшие тогда зеленый Мидлендс Англии. Их цель состояла в том, чтобы рассчитать, как наука может наилучшим образом поддержать продолжающуюся промышленную революцию с помощью новых методов, лучших инструментов и более точного планирования.
Задолго до поступления в Кембридж Бэббидж придумал способ ходить по воде. «Мой план, — писал он, — состоял в том, чтобы прикрепить к каждой ступне две доски, тесно соединенные между собой петлями, прикрепленными к подошве обуви». Эта штука работала достаточно хорошо, чтобы юный Чарльз хлюпал вниз по течению во время отлива. Но что-то пошло не так, и ему пришлось плыть, спасая свою жизнь.
«Мой план, — писал он, — состоял в том, чтобы прикрепить к каждой ступне две доски, тесно соединенные между собой петлями, прикрепленными к подошве обуви». Эта штука работала достаточно хорошо, чтобы юный Чарльз хлюпал вниз по течению во время отлива. Но что-то пошло не так, и ему пришлось плыть, спасая свою жизнь.
Он покинул Кембридж, одержимый идеей использования машин для ускорения трудоемких математических вычислений. Так родилась идея разностной машины. Чарльз также представил себе машину, которая будет обрабатывать больше знаков после запятой, чтобы ускорить процесс «переноса» и «заимствования».»
«Он всегда был великим изобретателем, — говорит Пегги Кидвелл, куратор Разностной машины Шойца в Смитсоновском институте. Кидвелл, соавтор книги «Вехи цифровых вычислений », считает, что Бэббиджа постоянно подстегивало стремление улучшить не только свой движок, но и качество жизни 19-го века. Среди других примеров она приводит его эксперименты с печатью таблиц разными цветами на бумаге разных оттенков (черный шрифт на белой бумаге сильно бросался в глаза). В 1826 году он опубликовал одну страницу таблиц 13 разными чернилами на бумаге 151 цвета.
В 1826 году он опубликовал одну страницу таблиц 13 разными чернилами на бумаге 151 цвета.
Что еще более важно, он бесконечно искал способы избавить заводскую работу от рутинной убийственной работы. Измерительные устройства, например, автоматически выполняли бы бессмысленный подсчет повторяющихся действий на мельнице. Он изобрел часы для отсчета времени; подозрительные работники назвали это «контрольным». Он разработал устройство для регистрации направления толчков в сейсмоопасных районах, красочный валик для печати и, возможно, думая о тех детских «водных туфлях», предложил идею гидроплана.
Он пытался заставить правительство изменить традиционные значения фунтов, шиллингов и пенсов на десятичную систему. Он достиг того же, что и американские ученые после многих лет тщетных мольб о введении метрической системы. Тем не менее, британцы приняли предложенную им монету в два шиллинга, или флорин, сделав десять флоринов равными фунту стерлингов.
Бэббидж так и не закончил полностью расширенную разностную машину, которую он начал называть «аналитической машиной», но части оригинала плавно отображались на дисплеях и продолжали привлекать к нему все больше внимания. «Теперь, мистер Бэббидж, — сказала одна женщина, выслушав его объяснения, — есть только одна вещь, которую я хочу знать. Если вы неправильно зададите вопрос, будет ли ответ правильным?» Со временем люди узнали, что компьютер не умнее своего программиста. Как говорится, «мусор на входе, мусор на выходе».
«Теперь, мистер Бэббидж, — сказала одна женщина, выслушав его объяснения, — есть только одна вещь, которую я хочу знать. Если вы неправильно зададите вопрос, будет ли ответ правильным?» Со временем люди узнали, что компьютер не умнее своего программиста. Как говорится, «мусор на входе, мусор на выходе».
Бэббидж был великолепным хозяином. Пришел герцог Веллингтон. Как и Чарльз Диккенс. Бэббидж говорил о делах с сэром Чарльзом Уитстоном, изобретателем моста Уитстона для измерения электрического сопротивления; с Джозефом Уитвортом, чья винтовочная пушка с шестигранным каналом ствола была куплена Конфедеративными Штатами Америки и использована со смертельной точностью против несчастных войск Союза; с Isambard Kingdom Brunel, строителем гигантского железного корабля Great Eastern ( Smithsonian , ноябрь 1994).
Прежде всего была Августа Ада Байрон, дочь поэта. Она была блестящей и красивой женщиной, которую Байрон назвал Августой в честь своей сводной сестры, которая также была его любовницей. Хотя Августа Ада была ее дочерью, леди Байрон так и не простила девушке того, что она носила то же имя, что и женщина, которую она презирала.
Хотя Августа Ада была ее дочерью, леди Байрон так и не простила девушке того, что она носила то же имя, что и женщина, которую она презирала.
Ада хорошо разбиралась в математике и была одной из немногих, кто мог понять и объяснить, в чем суть изобретений Бэббиджа. Это был целомудренный роман — Ада была замужем за графом Лавлейсом.Но она посвятила годы помощи Бэббиджу, написав объяснения его достижений и мечтаний, восхищаясь им как с профессиональной, так и с сыновней преданностью. Она написала некоторые из его заметок так хорошо, что он захотел опубликовать их под ее подписью. Она отказалась. Тем не менее, когда он немного переписал ее копию — всего лишь изменив пару слов, — она ясно дала понять, что никто никогда не переписывает Байрона.
Как и многие викторианцы, Ада пристрастилась к опиуму. Во время ее мрачной смерти от рака ее мать спрятала опиум, который она тогда использовала, чтобы облегчить боль, чтобы Ада страдала больше — и раскаялась.Ее смерть лишила Бэббиджа женщины, которую Энтони Хайман описывает как «свою любимую переводчицу». В его планы входило создание системы перфокарт, которая управляла бы функциями все еще теоретической машины. Идею карты он получил от известного французского ткацкого станка, представленного в начале 1800-х годов Жозефом Мари Жаккаром, который использовал выбранные карты для автоматизации плетения разноцветных узоров. Именно Ада могла лучше всего выразить то, что карточная система могла бы сделать для машины Шарля: «Мы можем наиболее точно сказать, что аналитическая машина ткет алгебраические узоры так же, как ткацкий станок Жаккарда ткет цветы и листья.»
В его планы входило создание системы перфокарт, которая управляла бы функциями все еще теоретической машины. Идею карты он получил от известного французского ткацкого станка, представленного в начале 1800-х годов Жозефом Мари Жаккаром, который использовал выбранные карты для автоматизации плетения разноцветных узоров. Именно Ада могла лучше всего выразить то, что карточная система могла бы сделать для машины Шарля: «Мы можем наиболее точно сказать, что аналитическая машина ткет алгебраические узоры так же, как ткацкий станок Жаккарда ткет цветы и листья.»
Хотя идеи Бэббиджа о хранении информации существуют только в его объемистых планах, его концепции продолжали приближаться к нашему компьютерному веку. Карточная система была жизненно важна для первых электронных компьютеров, устройств после Второй мировой войны, которые заполняли целую комнату.
Разностная машина Шойца также связывает нас с ранними днями существования Смитсоновского института. Джозеф Генри, первый секретарь Института, посетил Бэббиджа в 1837 году и написал: «Он, пожалуй, больше, чем любой из когда-либо живших людей, сузил пропасть, [разделяющую] науку и практическую механику. » Мягкая оценка. Судя по Бэббиджу сегодня, когда вокруг нас вращаются компьютеры, делая возможным жизненный опыт, простирающийся от космических полетов до Интернета, трудно не смотреть на этого пророка 19-го века с изумленным благоговением.
» Мягкая оценка. Судя по Бэббиджу сегодня, когда вокруг нас вращаются компьютеры, делая возможным жизненный опыт, простирающийся от космических полетов до Интернета, трудно не смотреть на этого пророка 19-го века с изумленным благоговением.
Рекомендуемые видео
№646: Отличие двигателя номер два
Сегодня больше об Аде, Бэббидже и мечте осуществленный. Колледж Университета Хьюстона Engineering представляет серию о машинах которые заставляют нашу цивилизацию работать, а людей чья изобретательность создала их.
Когда Чарльз
Бэббидж умер в 1871 году, оставив после себя загадочный массив
незавершенных счетных машин.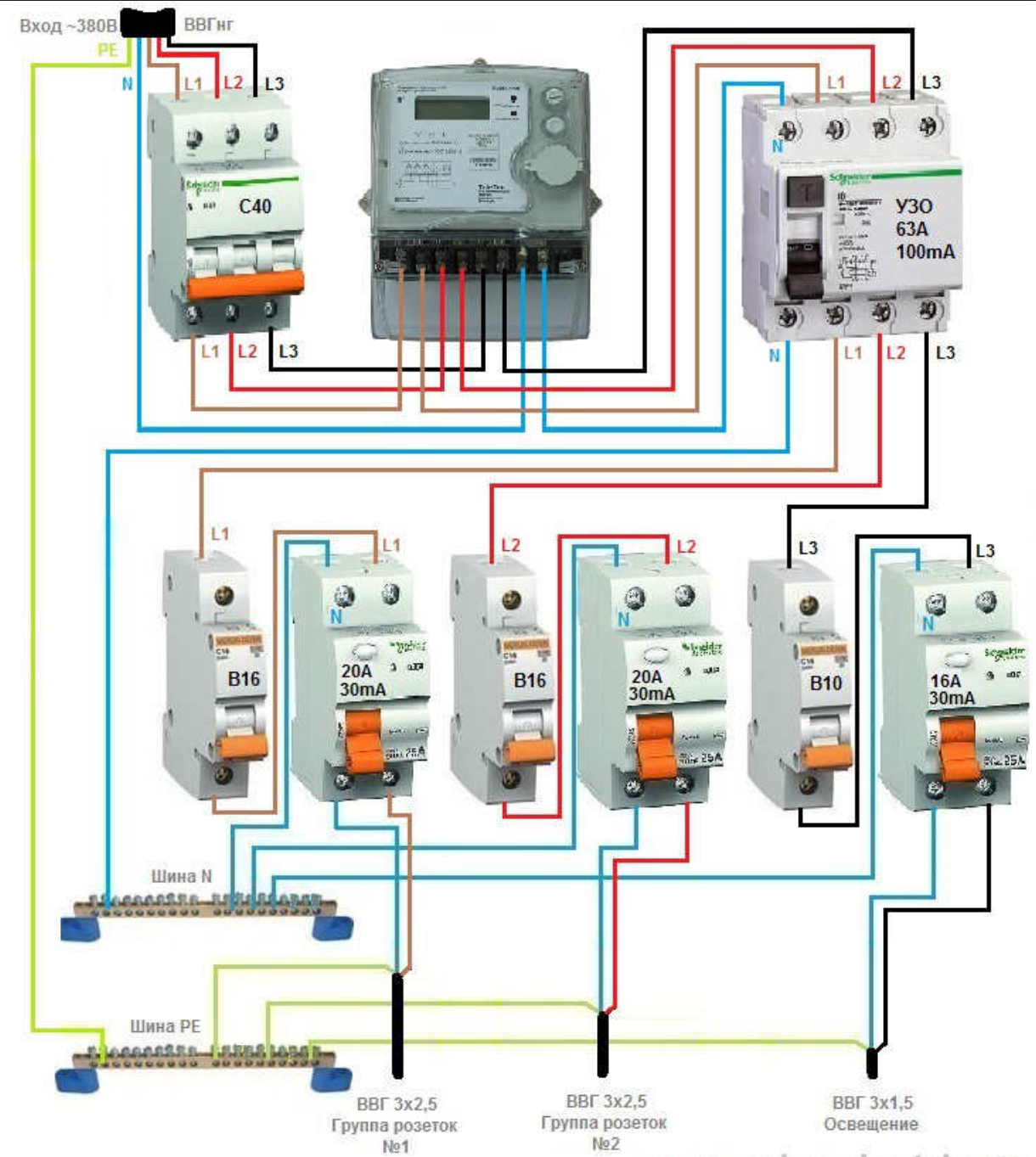 Они попали в
два класса — разностные машины и аналитические
двигатели. Его разностные двигатели предназначались для
вычислять математические таблицы — логарифмы и триггеры
функции. Его аналитические машины были бы
первые компьютеры, если они когда-либо были построены.
Они попали в
два класса — разностные машины и аналитические
двигатели. Его разностные двигатели предназначались для
вычислять математические таблицы — логарифмы и триггеры
функции. Его аналитические машины были бы
первые компьютеры, если они когда-либо были построены.
Он так и не закончил ни один из своих двигателей. Его финансирование всегда выбегал.Он сделал только части каждого вида. Хуже того, он мало писал о том, что делал. дочь лорда Байрона Ада много сделал для объяснения класса аналитических двигатели. Она опубликовала серию заметок о концепция.
Кажется довольно очевидным, что вдовец Бэббидж
любил Ада. Но Ада была замужем. Когда она умерла,
еще молодой, от рака, ее мать уничтожила любую
ее корреспонденции от Бэббиджа. Итак, нам осталось
угадать.
Итак, нам осталось
угадать.
Что касается Ады, то она любила математику и делала ставки на лошади. Вероятно, она тоже любила Бэббиджа. Сбрасывать многому научилась у него в математике. Она помогла сохранить его наследие, но она рассказала нам только о его аналитических машинах. Что насчет его разница двигателей?
Группа в Лондонском музее науки на самом деле построил последний двигатель Бэббиджа — его Отличие № двигателя2. Это стоило полмиллиона долларов, и он весит три тонны.
И это действительно работает. Он может вычислять числа до 31
десятичные разряды. Это гораздо точнее, чем ваш
карманный калькулятор. Конечно, это намного медленнее. Это бы
нужно 22 часа проворачивать вручную, чтобы получить это
результат. Сейчас музей пытается поднять еще один
360 000 долларов на создание принтера, предназначенного для Бэббиджа.
смирись с этим.
Это бы
нужно 22 часа проворачивать вручную, чтобы получить это
результат. Сейчас музей пытается поднять еще один
360 000 долларов на создание принтера, предназначенного для Бэббиджа.
смирись с этим.
В музее использованы материалы 19 века и технологии. Мозг Бэббиджа не только век опередил свое время. Теперь мы видим, что Бэббидж действительно могли бы построить компьютеры с 19-м веком ресурсов, если бы только он мог собрать эти Ресурсы.
В течение многих лет мы знали о так называемом Аналитическая машина.На самом деле это был не один двигатель, но класс компьютеров. Он построил части своего аналитические машины так же, как он построил части своего разница двигателей.
Заметки Ады Байрон исправили аналитическую машину в
наш разум как единая машина. Она оставила нас с
острое чувство незавершенного дела. Но, сосредоточившись
наше видение Бэббиджа, она также ограничила его.Сейчас мы
начинают видеть, что он был даже более продвинутым, чем мы
осуществленный. Получив немного больше государственного финансирования, он
могло бы изменить ход истории.
Она оставила нас с
острое чувство незавершенного дела. Но, сосредоточившись
наше видение Бэббиджа, она также ограничила его.Сейчас мы
начинают видеть, что он был даже более продвинутым, чем мы
осуществленный. Получив немного больше государственного финансирования, он
могло бы изменить ход истории.
Я Джон Линхард из Хьюстонского университета. где нас интересует, как изобретательные умы Работа.
(Музыкальная тема)Удивительная аналитическая машина — как она работает — 2D-очки
Привет всем! Как и было обещано: аналитическая машина Бэббиджа, как, черт возьми, она работает?
Если вы новичок на этом веб-сайте, возможно, вы лишь смутно осведомлены о чудесной, но таинственной аналитической машине Чарльза Бэббиджа, первой конструкции настоящего компьютера, созданной в 1840-х годах. У него были программы, память, циклы, циклы и всевозможные компьютерные штуки, несмотря на то, что он был полностью построен из латунных шестерен и приводился в движение паровым двигателем. Когда я начал этот комикс, я был крайне разочарован расплывчатостью почти каждого его описания. В конце концов мне пришлось создать свой собственный в компьютерной форме (какой мета!). Я обнаружил, что это не только восхитительно красивая машина, напичканная хитроумными устройствами, но и гораздо более простая для понимания, чем современный компьютер.Как, черт возьми, работают эти штуки?
У него были программы, память, циклы, циклы и всевозможные компьютерные штуки, несмотря на то, что он был полностью построен из латунных шестерен и приводился в движение паровым двигателем. Когда я начал этот комикс, я был крайне разочарован расплывчатостью почти каждого его описания. В конце концов мне пришлось создать свой собственный в компьютерной форме (какой мета!). Я обнаружил, что это не только восхитительно красивая машина, напичканная хитроумными устройствами, но и гораздо более простая для понимания, чем современный компьютер.Как, черт возьми, работают эти штуки?
Захватывающие приключения имеет приложение со множеством диаграмм и объяснений того, как работает аналитическая машина и как она связана с современными компьютерами, но я думаю, что, несмотря на удовольствие от печати, общая работа машины наиболее ясно объясняется анимацией. Я надеюсь, что это видео сделает его более понятным — я должен подчеркнуть, что а) это суперупрощенная, карикатурная, урезанная версия, и б) это лучшее, что я понимаю, почерпнутое из бумаг покойного Аллана Бромли (одолжил мне Джон Грэм-Камминг, спасибо, Джон, и я полностью возвращаю их, клянусь!!), который написал, я думаю, самые полные современные описания двигателя. Я могу быть СОВСЕМ НЕПРАВИЛЬНЫМ во многих вещах. Итак, начнем (я гм и ээ намного меньше после первых нескольких минут, я обещаю…):
Я могу быть СОВСЕМ НЕПРАВИЛЬНЫМ во многих вещах. Итак, начнем (я гм и ээ намного меньше после первых нескольких минут, я обещаю…):
Историческая справка: у меня был момент сестринства с Адой Лавлейс, когда я писал, как работает Двигатель. В ее переписке с Бэббиджем во время написания ее знаменитых «Заметок об эскизе аналитической машины» между ними происходит небольшая переписка, четко отображающая их характеры. Бэббидж пишет:
Существует еще одно пустяковое недоразумение относительно карт Переменных — Карта Переменных может приказать любому количеству Переменных получить такое же число в один и тот же момент времени — Но карта Переменных никогда не может быть направлена на заказ более чем одной Переменной отдавать сразу, потому что мельница не могла его принять, а механизм не позволял.Все это вы не могли знать интуитивно, и чем больше я читаю ваши Заметки, тем больше удивляюсь им и жалею, что раньше не исследовал столь богатую жилу благороднейшего металла.
На что Лавлейс отвечает беспокойным тоном, знакомым человеку, погребенному под сваями Диаграммы аналитической машины:
Я не могу понять, что вы имеете в виду насчет переменных карт; так как я никогда не предполагал в своем уме, что одна карта Переменных может выдать более одной Переменной за раз; и (насколько я могу судить) не выражал такой мысли ни в каком отрывке.
Это то, на что можно равнодушно поглядывать, читая историческую переписку, пока не поймаешь себя на том, что пишешь: «Переменные карты затем считывают числа на адресах в Мельницу»… и затем скрупулезно добавляют «ОДНО ЗА РАЗ». как призрак Чарльза Бэббиджа тревожно витает над чьим-то плечом…
В любом случае, если вы очень увлечены этим и хотите увидеть специфику некоторых из тысяч маленьких рычагов, вот видео о предвосхищающей каретке для их переноски (в котором, кстати, все еще упущены некоторые детали).Бэббидж был бы вне себя от восторга, узнав, что первый вопрос, который я задал в своем выступлении о комиксе в Google, был о том, как он планирует носить их! Эта часть Двигателя была самым гордым достижением Бэббиджа, он назвал это «обучением Двигателя предвидеть и действовать в соответствии с этим предвидением».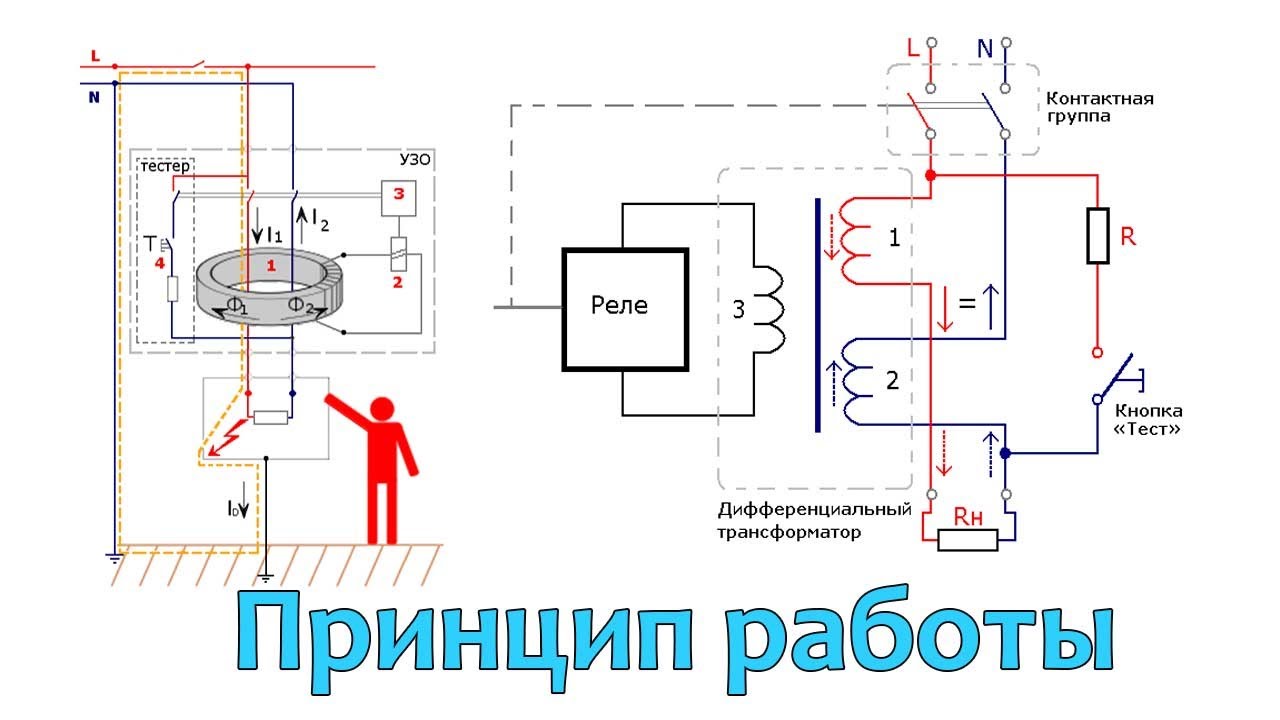
(У меня есть еще несколько видео на Engine на YouTube, хотя в них меньше объяснений, которые вы можете считать особенностью.)
Получите ваши прекрасные горячие отпечатки аналитической машины!
ТАКЖЕ — по многочисленным просьбам теперь вы можете купить отпечатки визуализации Analytical Engine в великолепном цвете Technicolor! (в предыдущем посте объяснялось, почему цвета, которые я выбрал для окраски двигателя, именно такие.. праздничный). У меня есть несколько новых дизайнов футболок и еще пара принтов в пути, как только у меня будет полсекунды, которой у меня сейчас нет.
Многие спрашивают, будут ли еще Лавлейс и Бэббидж? Ответ ДА! Но вам придется продержаться ЕЩЕ пару месяцев. Как некоторые из вас, возможно, знают, ночью я всего лишь бесстрашный рисующий комедии; днем я сражаюсь с гигантскими монстрами в очаровательном, но ужасающем колизее анимации визуальных эффектов.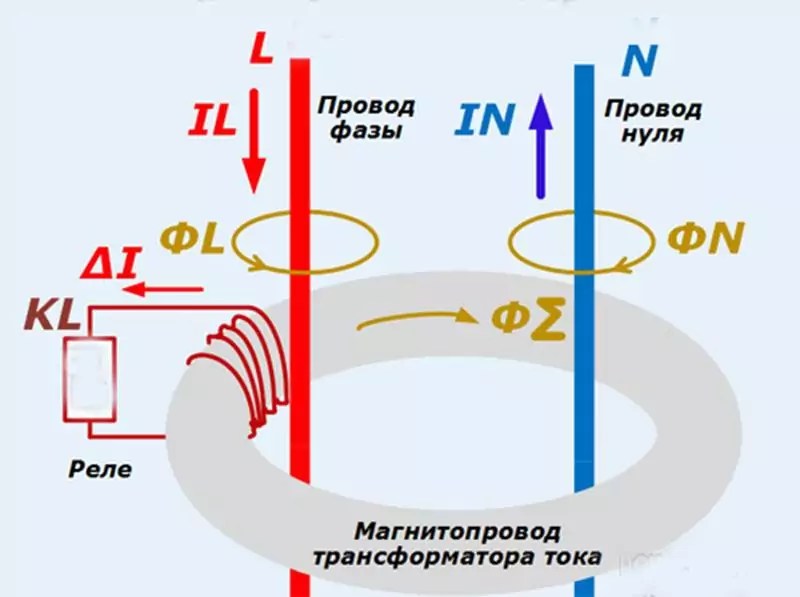
А пока вы можете полюбоваться моими развевающимися волосами и вконец надоесть моим невыносимым писклявым голосом на нескольких интервью (неполный список.. еще больше впереди!), наследие моего книжного тура по Doom, о котором я должен рассказать вам все когда-нибудь, когда у меня будет секунда. Кроме того, я с облегчением сообщаю, что после того, как я был готов к кирпичным битам и насмешкам, если не к полной озадаченной тишине, вышла целая куча отличных обзоров для Захватывающие приключения Лавлейса и Бэббиджа — ссылки на кучу внизу этого страница.
И, НАКОНЕЦ, .. если вы будете в Лондоне в ближайшие выходные, вы можете поймать меня на Литературном фестивале в Сток-Ньюингтоне на панели комиксов в воскресенье.
Кем был Чарльз Бэббидж? | ИНСТИТУТ ЧАРЛЬЗА БЭББИДЖА
Вычислительные машины английского математика Чарльза Бэббиджа (1791-1871) являются одними из самых знаменитых икон в предыстории вычислительной техники. Разностная машина № 1 Бэббиджа была первым успешным автоматическим калькулятором и остается одним из лучших образцов точной инженерии того времени. Бэббиджа иногда называют «отцом вычислительной техники». Международное общество Чарльза Бэббиджа (позже Институт Чарльза Бэббиджа) взяло его имя в честь его интеллектуального вклада и их связи с современными компьютерами.
Бэббиджа иногда называют «отцом вычислительной техники». Международное общество Чарльза Бэббиджа (позже Институт Чарльза Бэббиджа) взяло его имя в честь его интеллектуального вклада и их связи с современными компьютерами.
Биография
Чарльз Бэббидж родился 26 декабря 1791 года в семье Бенджамина Бэббиджа, лондонского банкира. В юности Бэббидж был своим собственным учителем алгебры, которую он страстно любил, и хорошо разбирался в континентальной математике своего времени. Поступив в Тринити-колледж в Кембридже в 1811 году, он оказался намного впереди своих наставников по математике. Бэббидж стал соучредителем Аналитического общества для продвижения континентальной математики и реформирования математики Ньютона, который тогда преподавал в университете.
В свои двадцать с небольшим Бэббидж работал математиком, главным образом в области исчисления функций. Он был избран членом Королевского общества в 1816 году и сыграл заметную роль в основании Астрономического общества (позже Королевского астрономического общества) в 1820 году. Примерно в это же время Бэббидж впервые заинтересовался вычислительными машинами, которые стали его всепоглощающим интересом. страсть на всю оставшуюся жизнь.
Примерно в это же время Бэббидж впервые заинтересовался вычислительными машинами, которые стали его всепоглощающим интересом. страсть на всю оставшуюся жизнь.
В 1821 году Бэббидж изобрел разностную машину для составления математических таблиц.Завершив ее в 1832 году, он задумал более совершенную машину, которая могла бы выполнять не одну математическую задачу, а любые вычисления. Это была аналитическая машина (1856 г.), которая задумывалась как универсальный манипулятор символов и имела некоторые характеристики современных компьютеров.
К сожалению, от прототипов вычислительных машин Бэббиджа мало что осталось. Критические допуски, требуемые его машинами, превышали уровень технологий, доступных в то время. И хотя работа Бэббиджа была официально признана уважаемыми научными учреждениями, британское правительство приостановило финансирование его разностной машины в 1832 году и после мучительного периода ожидания прекратило проект в 1842 году.Остались только фрагменты прототипа разностной машины Бэббиджа, и хотя он посвятил большую часть своего времени и большого состояния созданию своей аналитической машины после 1856 года, ему так и не удалось завершить ни один из своих нескольких проектов для нее. Джордж Шойц, шведский печатник, успешно сконструировал машину на основе конструкции разностной машины Бэббиджа в 1854 году. Эта машина печатала математические, астрономические и актуарные таблицы с беспрецедентной точностью и использовалась британским и американским правительствами.Хотя работа Бэббиджа была продолжена его сыном Генри Прево Бэббиджем, после его смерти в 1871 году аналитическая машина так и не была успешно завершена и запускала лишь несколько «программ» с досадно очевидными ошибками.
Джордж Шойц, шведский печатник, успешно сконструировал машину на основе конструкции разностной машины Бэббиджа в 1854 году. Эта машина печатала математические, астрономические и актуарные таблицы с беспрецедентной точностью и использовалась британским и американским правительствами.Хотя работа Бэббиджа была продолжена его сыном Генри Прево Бэббиджем, после его смерти в 1871 году аналитическая машина так и не была успешно завершена и запускала лишь несколько «программ» с досадно очевидными ошибками.
Бэббидж занимал Лукасовскую кафедру математики в Кембридже с 1828 по 1839 год. Он сыграл важную роль в создании Ассоциации развития науки и Статистического общества (позже Королевского статистического общества). Он также пытался реформировать научные организации того периода, призывая правительство и общество выделять больше денег и престижа научной деятельности.На протяжении всей своей жизни Бэббидж работал во многих интеллектуальных областях, типичных для его времени, и внес вклад, который обеспечил бы его известность независимо от разностных и аналитических машин.
Несмотря на его многочисленные достижения, неудача в создании вычислительных машин и, в частности, неспособность правительства поддержать его работу, сделали Бэббиджа на склоне лет разочарованным и озлобленным человеком. Он умер в своем доме в Лондоне 18 октября 1871 года.
Дифференциальное машинное обучение.Необоснованно эффективная функция… | Антуан Савин
Необоснованно эффективная аппроксимация функций с помощью нового использования производных
5-минутный видеообзор, записанный для семинара Bloomberg по барбекю 28 мая 2020 г. Мы с Брайаном Хьюгом только что опубликовали рабочий документ после шести месяцев исследований и разработок в области аппроксимации функций с помощью искусственного интеллекта. (AI) в Danske Bank. Одним из основных выводов было то, что обучающие модели машинного обучения (ML) для регрессии (т. е. прогнозирования значений, а не классов) могут быть значительно улучшены, когда доступны градиенты обучающих меток относительно обучающих входных данных . Учитывая эти дифференциальных меток , мы можем написать простые, но необоснованно эффективные алгоритмы обучения, способные изучать точные аппроксимации функций с замечательной скоростью и точностью из небольших наборов данных стабильным образом, без необходимости дополнительной регуляризации или оптимизации гиперпараметров, например. перекрестной проверкой.
Учитывая эти дифференциальных меток , мы можем написать простые, но необоснованно эффективные алгоритмы обучения, способные изучать точные аппроксимации функций с замечательной скоростью и точностью из небольших наборов данных стабильным образом, без необходимости дополнительной регуляризации или оптимизации гиперпараметров, например. перекрестной проверкой.
В этом посте мы кратко суммируем эти алгоритмы под названием дифференциального машинного обучения , выделяя основные интуитивные идеи и преимущества и комментируя код реализации TensorFlow.Все детали можно найти в рабочем документе, онлайн-приложениях и блокнотах Colab.
В контексте аппроксимации цен на финансовые деривативы обучающие наборы моделируются с помощью моделей Монте-Карло. Каждый обучающий пример моделируется на одном пути Монте-Карло, где метка — это конечный выигрыш транзакции, а вход — вектор начального состояния рынка. Дифференциальные метки представляют собой путевых градиентов выигрыша по отношению к состоянию и эффективно вычисляются с помощью автоматического сопряженного дифференцирования (AAD). По этой причине дифференциальное машинное обучение особенно эффективно в финансах, хотя оно также применимо во всех других ситуациях, когда доступны высококачественные производные первого порядка относительно входных данных для обучения.
По этой причине дифференциальное машинное обучение особенно эффективно в финансах, хотя оно также применимо во всех других ситуациях, когда доступны высококачественные производные первого порядка относительно входных данных для обучения.
Модели обучаются на расширенных наборах данных не только входных данных и меток, но и дифференциалов:
путем минимизации совокупной стоимости ошибок прогнозирования на значениях и производных :
Значение и производное метки заданы.Мы вычисляем предсказанных значений путем вывода, как обычно, и предсказанных производных путем обратного распространения. Хотя эта методология применима к архитектурам произвольной сложности, мы обсуждаем ее здесь в контексте ванильных сетей с прямой связью в интересах простоты.
Вспомните ванильные уравнения прямой связи:
уравнений прямой связи, где обозначения стандартны и указаны в статье (индекс 3 для соответствия статье).
Весь код в этом посте взят из демонстрационной записной книжки, которая также включает комментарии и детали практической реализации. Стандартный импорт
Стандартный импорт
Ниже приведена реализация TensorFlow (1.x) уравнений прямой связи. Мы решили явно написать матричные операции вместо высокоуровневых слоев Keras, чтобы выделить уравнения в коде. Мы выбрали активацию softplus. ELU — еще одна альтернатива. По причинам, объясненным в статье, активация должна быть непрерывно дифференцируемой, исключая, например, РЕЛУ и СЕЛУ.
уравнений прямой связи в кодеПроизводные выходных данных относительно входных данных прогнозируются с обратным распространением.Вспомним, что уравнения обратного распространения получаются как сопряженных уравнений прямого распространения, или см. наш учебник для обновления:
уравнение обратного распространенияИли в коде, напомнив, что производная softplus является сигмовидной:
уравнений обратного распространения в коде Еще раз, мы написали уравнения обратного распространения явно вместо вызова tf.gradients() . Мы решили сделать это таким образом, во-первых, чтобы снова выделить уравнения в коде, а также, чтобы избежать вложения слоев обратного распространения во время обучения, как показано далее. Во избежание сомнений, замена этого кода одним вызовом tf.gradients() тоже работает.
Во избежание сомнений, замена этого кода одним вызовом tf.gradients() тоже работает.
Затем мы объединяем прямое распространение и обратное распространение в одной сети , которую мы называем сетью-близнецом , нейронной сетью в два раза большей глубины, способной одновременно предсказывать значения и производные за удвоенную стоимость вычислений: комбинация прямого и обратного распространения
Двойная сеть выгодна по двум причинам. После обучения он эффективно предсказывает значения и производные с учетом входных данных в приложениях, где желательны предсказания производных. В финансах, например, это чувствительность цен к переменным состояния рынка, также называемые греками (потому что трейдеры дают им греческие буквы), а также соответствующие коэффициенты хеджирования .
Двойная сеть также является фундаментальной конструкцией для дифференциального обучения . Комбинированная функция стоимости вычисляется путем логического вывода через двойную сеть, прогнозируя значения и производные. Градиенты функции стоимости вычисляются путем обратного распространения через двойную сеть, включая часть обратного распространения, незаметно выполняемую TensorFlow как часть его цикла оптимизации. Вспомним стандартный цикл обучения для нейронных сетей:
Градиенты функции стоимости вычисляются путем обратного распространения через двойную сеть, включая часть обратного распространения, незаметно выполняемую TensorFlow как часть его цикла оптимизации. Вспомним стандартный цикл обучения для нейронных сетей:
Дифференциальный цикл обучения практически идентичен, безопасен для определения функции стоимости, теперь он объединяет среднеквадратические ошибки значений и производных:
дифференциальный цикл обученияTensorFlow различает близнеца сеть легко за кулисами для нужд оптимизации.Неважно, что часть сети сама по себе является обратным распространением. Это просто еще одна последовательность матричных операций, которую TensorFlow различает без труда.
Остальная часть записной книжки посвящена стандартной подготовке данных, обучению и тестированию, а также применению к паре наборов данных из учебников по финансам: европейские звонки в Black & Scholes и опционы на корзину в коррелированном Bachelier. Результаты демонстрируют необоснованную эффективность дифференциального глубокого обучения.
Результаты демонстрируют необоснованную эффективность дифференциального глубокого обучения.
Дифференциальное обучение накладывает штраф на неправильные производные точно так же, как традиционная регуляризация, такая как гребень/Тихонов, способствует малым весам. В отличие от обычной регуляризации, дифференциальный ML эффективно уменьшает переоснащение без введения смещения .Следовательно, нет компромисса между смещением и дисперсией или необходимости настраивать гиперпараметры путем перекрестной проверки. Это просто работает.
Дифференциальное машинное обучение больше похоже на дополнение данных , которое, в свою очередь, можно рассматривать как лучшую форму регуляризации. Увеличение данных последовательно применяется, например. в компьютерном зрении с задокументированным успехом. Идея состоит в том, чтобы создать несколько помеченных изображений из одного, например.




 )
)